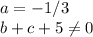Answer:
(a)
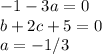
(b)
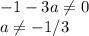
(c)
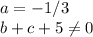
Explanation:
The first thing you have to do is write the problem in matrix terms and then reduce the matrix.
The system of equations on matrix notation looks like this.
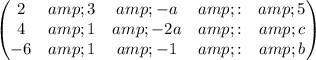
When you write the matrix like that you then reduce it using elementary row operations. After you reduce the matrix it looks like this
After you use reduce the matrix using Gaussian elimination (I attach images with the steps) you get the following matrix.
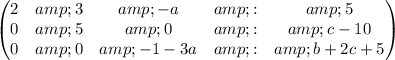
(a)
Now, if you want a unique solution, you must be able by -1-3a. That last part of means
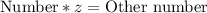 , so in order to solve that equation, your "Number" must be zero and the "Other number" must also be zero, that is something which is always true 0=0 therefore it has infinite solutions. Then
, so in order to solve that equation, your "Number" must be zero and the "Other number" must also be zero, that is something which is always true 0=0 therefore it has infinite solutions. Then
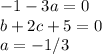
(b)
For this part your "Number" must be different than zero so you can divide by it . Therefore
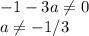
(c) For this part your your "Number" must be zero and the other number must be something different than zero, so you get something which is not true like 0 = 4. Therefore