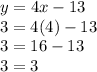Answer:
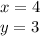
Explanation:
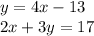
Since our ''y'' is already isolated, you can simply plug ''y'' information into the second equation.
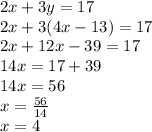
Now we can use the first equation and replace ''x'' to find ''y''
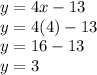
To prove that your values are correct, take any of the equations and replace their values.