Question

Consider a call center with three identical agents (servers) and four phone lines. Call arrivals follow a Poisson process with rate 2 per minute. An arriving call that finds all lines busy is lost (blocked). Call processing times are i.i.d., exponentially distributed with mean 1 minute. An admitted call that finds all agents busy will wait until getting service, occupying a phone line. Model this system as a CTMC.

1.Find the long-term throughput of the system (the rate of served customers leaving the system).

2.Find the average waiting time (in queue) among those who are served. Find the average number of calls in the entire system.

Answer 1

1. the rate of served customer leaving the system is 13/9

2. average waiting time in queue is 4/9 minutes

average number of calls in the entire system is 26/9 = 2.889 calls

Explanation:

hello,

The queuing model is a 3 channel or server model. We will use the following notations in solving the question;

M= Number of servers which is 3

λ= average arrival rate = 2 minutes

μ = average service rate at each server = 1 minute

please note that the rate of served customers leaving the system is the same as the average rate a customers spends in waiting line and being served (or in other words the average time spent in the system)

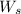`W_s`= the rate of served calls leaving the system

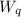`W_q`= average waiting time in queue.

L = average number of calls in the system.

To solve this we must first find the probability, P that there are 0 call in the system. please see the first attached file for the formula to find P.

Thus we have;

`P=(1)/([\sum_(n=0)^(n=2)(1)/(n!) ((2)/(1) )^n] +(1)/(3!)((2)/(1) )^3 ((3)(1))/((3)(1)- 2) )`

`P=(1)/([1+2+2] + (8)/(6)(3) )`

`P=(1)/(5+4) = (1)/(9)`

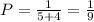
2. we will find the average number of calls in the entire system for this will be used for find the rate of served customers leaving the system. please see the second attached file for the formula for the average number of calls in the entire system.

`L=((2)(1)((2)/(1) )^3)/((3-1)! ((3)(1)- 2)^2) ((1)/(9) ) + ((2)/(1))`

`L=(16)/(2) ((1)/(9) ) +(2 ) = (26)/(9) = 2.889 \ \ $calls$`

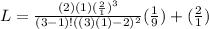
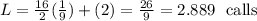
Next we find the rate of served customers leaving the system.

please see the third attached file for the formula of the rate of served customers leaving the system.

`W_s=((26)/(9) )/(2) = (13)/(9) \ $minutes$`

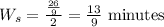
finally we find the average waiting time in queue.

please see the fourth attached file for the formula of the average waiting in queue.

`W_q=(13)/(9) - 1 = (4)/(9) \ $minutes$`