Question

A local supermarket is trying to sell treadmill, but he needs to decide whether to sell brand A or brand B. To help arrive at a decision, an experiment is conduct using randomly selected 12 months' sales volume of each brand. For each brand, the sales volume for a month is the total amount of sales during that month. Test the hypothesis that the brand A's sales volume is different from brand B's with α = 0.05. Assume the populations to be independent and approximately normally distributed. Following R code may or may not be helpful.> brandA <- c(36720.48, 30245.67, ....)> brandB <- c(33132.05, 42034.55, ....)> mean(brandA) = 35841> mean(brandB) = 37449> sd(brandA) = 5075> sd(brandB) = 6884> sd(brandA-brandB) = 10381a) Specify the assumptions and the hypotheses.b) Calculate the test statistic.c) Report the p-value. Following R code may or may not be helpful.> pt(-0.536, df=11) = 0.301> pt(-0.651, df=11) = 0.264> pnorm(-0.536)= 0.295> pnorm(-0.651) = 0.257

Answer 1

(a) Null Hypothesis,
`H_0` :
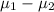`\mu_1-\mu_2` = 0 or
`\mu_1= \mu_2`

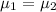
Alternate Hypothesis,
`H_A` :
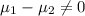`\mu_1-\mu_2\\eq 0` or
`\mu_1\\eq \mu_2`

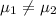
(b) The test statistic is 0.651.

(c) The p-value is 0.261.

Explanation:

We are given that a local supermarket is trying to sell treadmill, but he needs to decide whether to sell brand A or brand B. To help arrive at a decision, an experiment is conduct using randomly selected 12 months' sales volume of each brand. For each brand, the sales volume for a month is the total amount of sales during that month.

Let
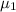`\mu_1` = mean sales volume of brand A

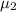`\mu_2` = mean sales volume of brand B

(a) Null Hypothesis,
`H_0` :
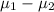`\mu_1-\mu_2` = 0 or
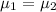`\mu_1= \mu_2` {means that the brand A's sales volume is same as that of brand B's}

Alternate Hypothesis,
`H_A` :
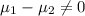`\mu_1-\mu_2\\eq 0` or
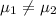`\mu_1\\eq \mu_2` {means that the brand A's sales volume is different from brand B's}

The test statistics that will be used here is Two-sample t test statistics as we don't know about the population standard deviations;

T.S. =
`\frac{(\bar X_1-\bar X_2)-(\mu_1-\mu_2)}{s_p\sqrt{(1)/(n_1)+(1)/(n_2) } }` ~
`t__n__1+_n__2-2`

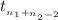
where,
`\bar X_1` = sample mean sales for brand A = 35,841

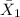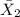`\bar X_2` = sample mean sales for brand B = 37,449

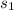`s_1` = sample standard deviation for brand A = 5,075

`s_2` = sample standard deviation for brand B = 6,884

`n_1` = sample of month's sales of brand A = 12

`n_2` = sample of month's sales of brand B = 12

Also,
`s_p=\sqrt{((n_1-1)s_1^(2)+(n_2-1)s_2^(2) )/(n_1+n_2-2) }` =
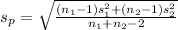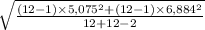`\sqrt{((12-1)* 5,075^(2)+(12-1)* 6,884^(2) )/(12+12-2) }` = 6047.52

(b) So, the test statistics =
`\frac{(35,841-37,449)-(0)}{6047.52 * \sqrt{(1)/(12)+(1)/(12) } }` ~
`t_2_2`

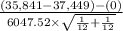= -0.651

(c) Now, P-value of the test statistics is given by the following formula;

P-value = P(
`t_2_2` > -0.651) = 0.261

Now at 0.01 significance level, the t table gives critical values between -2.074 and 2.074 at 22 degree of freedom for two-tailed test. Since our test statistics lies within the range of critical values of t, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.

Therefore, we conclude that the brand A's sales volume is same as that of brand B's.