Question

The data (1.5.8.5.1) represent a random sample of the number of days absent from school for five students at Monta Vista High. Find the

mean and standard deviation of the data.
Select one
a. mean = 4; standard deviation = 2.68
b.mean = 4: standard deviation = 7.2
c. mean = 20; standard deviation = 7.6
d. mean = 4.4; standard deviation = 2.76

Answer 1

`\bar X = (1+5+8+5+1)/(5)= (20)/(5)= 4`

`\sigma= \sqrt{((1-4)^2 +(5-4)^2 +(8-4)^2 +(5-4)^2 +(1-4)^2)/(5)} =\sqrt{(36)/(5)}= 2.68`

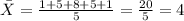
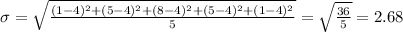
And based on this the best answer would be:

a. mean = 4; standard deviation = 2.68

Explanation:

For this case we have the following data given:

1,5,8,5,1

We can find the sample mean with the following formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And replacing we got:

`\bar X = (1+5+8+5+1)/(5)= (20)/(5)= 4`

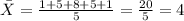
And for the deviation (assuming that the correct approximation is the deviation for a population) we can calculate the deviation with the following formula:

`\sigma = \sqrt{(\sum_(i=1)^n (X_i -\bar X)^2)/(n)}`

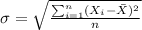
And replacing we got:

`\sigma= \sqrt{((1-4)^2 +(5-4)^2 +(8-4)^2 +(5-4)^2 +(1-4)^2)/(5)} =\sqrt{(36)/(5)}= 2.68`

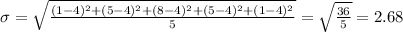
And based on this the best answer would be:

a. mean = 4; standard deviation = 2.68