Question:
Winter visitors are extremely important to the economy of southwest Florida. hotel occupancy is an often-reported measure of visitor volume and activity. Hotel occupancy data for February in two consecutive years are as follows
Current Year Previous Year
Occupied Rooms 1470 1458
Total Rooms 1750 1800
a. Formulate the hypothesis test that can be used to determine if there has been an increase in the proportion of rooms occupied over the one-year period.
b. What is the estimated proportion of hotel rooms occupied each year?
c. Using a 0.05 level of significance, what is your hypothesis test conclusion? What is the p-value?
d. What is the 95% confidence interval estimate of the change in occupancy for the one-year period? Do you think area officials would be pleased with the results?
Answer:
a. Null hypothesis H₀ : P₁ = P₂
Alternative hypothesis Hₐ : P₁ < P₂
b. Proportion of occupied room in previous year is 0.84
Proportion of occupied room in current year is 0.81
c. There is sufficient statistical evidence to suggest that there has not been an increase in the proportion of rooms occupied over the one year period
p-value is 0.991
d. Minimum ΔP is 0.005031
Maximum ΔP is 0.055
ΔP is P₁ - P₂
The officials will not be pleased
Explanation:
a. The hypothesis to be tested are;
Null hypothesis H₀ : P₁ = P₂
Alternative hypothesis Hₐ : P₁ < P₂
Where:
P₁ = Proportion of occupied room in previous year
P₂ = Proportion of occupied room in current year
b. The estimated proportion of occupied rooms is given by the following relation;
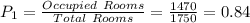
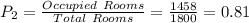
c. The hypothesis test formula is given as follows;
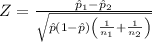
Where
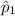 = P₁
= P₁
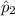 = P₂
= P₂
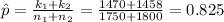
n₁ = 1750
n₂ = 1800
Plugging the values give;
Z = 2.350769
Looking up the value of Z based on normal distribution relation gives the probability, p =0.991
Therefore, since p > α = 0.05, we fail to reject the null hypothesis, that is there is sufficient statistical evidence to suggest that there has not been an increase in the proportion of rooms occupied over the one year period
The p-value = 0.991
d. The 95% confidence interval is given by the following relation;
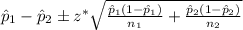
Z at 95% = 1.96
Plugging the values give;
Minimum ΔP = 0.005031
Maximum ΔP = 0.055
Where;
ΔP = P₁ - P₂
The officials will not be pleased given that ΔP = P₁ - P₂, which shows that P₁ > P₂.