Question

In ΔCDE, the measure of ∠E=90°, the measure of ∠D=44°, and DE = 2.8 feet. Find the length of EC to the nearest tenth of a foot.

Answer 1

Given:

Given that ΔCDE is a right triangle.

The measure of ∠E is 90°

The measure of ∠D is 44° and the length of DE is 2.8 feet.

We need to determine the length of EC.

Length of EC:

The length of EC can be determined using the trigonometric ratio.

Thus, we have;

`tan \ \theta=(opp)/(adj)`

where θ = D, the side opposite to angle D is EC and the side adjacent to angle D is ED.

Substituting the values, we have;

`tan \ D=(EC)/(ED)`

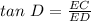
Substituting the lengths, we get;

`tan \ 44^(\circ)=(EC)/(2.8)`

Multiplying both sides of the equation by 2.8, we have;

`tan \ 44^(\circ)* 2.8 = EC`

`2.7=EC`

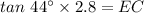
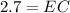
Thus, the length of EC is 2.7 feet.