Question

Devin has a collection of 40 model vehicles which consists of 25 different cars and 15 different trucks. He selects 8 to display on the shelf in his room. How many different ways can he select 3 cars and 5 trucks?

Answer 1

The number of ways to select 3 cars and 5 trucks is 69,06,900.

Explanation:

In mathematics, the procedure to select k items from n distinct items, without replacement, is known as combinations.

The formula to compute the combinations of k items from n is given by the formula:

`{n\choose k}=(n!)/(k!(n-k)!)`

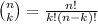
It is provided that:

Number of different cars, n (C) = 25.

Number of different trucks, n (T) = 15.

Devin selects 8 vehicles to display on the shelf in his room.

Compute the number of ways in which he can select 3 cars from 25 different cars as follows:

`{25\choose 3}=(25!)/(3!(25-3)!)=(25*24*23*22!)/(3!*22!)=2300`

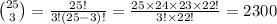
There are 2300 ways to select 3 cars.

Compute the number of ways in which he can select 5 trucks from 25 different trucks as follows:

`{15\choose 5}=(15!)/(5!(15-5)!)=(15*14*13*12* 11*10!)/(5!*10!)=3003`

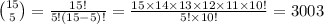
There are 3003 ways to select 5 trucks.

Compute the total number of ways to select 3 cars and 5 trucks as follows:

n (3 cars and 5 trucks) = n (3 cars) × n (5 trucks)

`={25\choose 3}* {15\choose 5}\\=2300* 3003\\=6906900`

Thus, the total number of ways to select 3 cars and 5 trucks is 69,06,900.