Question

"The CEO of a large electric utility claims that 80% of all his customers are very satisfied with the service they receive. To test this claim, the local newspaper surveyed 100 customers, using simple random sampling. Among the sampled customers, 73% say they are very satisfied. Were these surveyed customers less likely to be satisfied than all the CEO’s customers ( \alpha =0.05)?"

Answer 1

The claim made by the CEO was correct.

Explanation:

The CEO of a large electric utility claims that 80% of all his customers are very satisfied with the service they receive.

A one-proportion z-test can be used to determine whether the claim made by the CEO of a large electric utility is correct or not.

The hypothesis can be defined as:

H₀: The proportion of customers that are very satisfied with the service they receive is 80%, i.e. p = 0.80.

Hₐ: The proportion of customers that are very satisfied with the service they receive is not 80%, i.e. p ≠ 0.80.

The information provided is:

`\hat p` = 0.73

n = 100

α = 0.05

Compute the test statistic as follows:

`z=\frac{\hat p-p}{\sqrt{(p(1-p))/(n)}}=\frac{0.73-0.80}{\sqrt{(0.80(1-0.80))/(100)}}=-1.75`

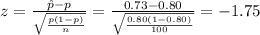
The test statistic value is -1.75.

The decision rule is:

If the p-value of the test is less than the significance level then the null hypothesis will be rejected and vice-versa.

Compute the p-value of the two-tailed test as follows:

`p-value=2* P(Z<-1.75)\\=2* [1-P(Z<1.75)]\\=2* [1-0.95994]\\=0.08012 \\\approx 0.08`

*Use a z-table for the probability.

The p-value of the two-tailed test is 0.08.

p-value = 0.08 > α = 0.05

The null hypothesis was failed to be rejected at 5% level of significance.

Thus, it can be concluded that the claim made by the CEO was correct. The proportion of customers that are very satisfied with the service they receive is 80%.