Answer:
The probability that the sum of Michelle's rolls is 4 is 0.083
∴ P(A)=0.083
Explanation:
Given that Michelle is rolling two six-sided dice, numbered one through six.
To find the probability that the sum of her rolls is 4:
![s={\{(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)}\}]()
∴ n(s)=36
Let P(A) be the probability that the sum of her rolls is 4
Then the possible rolls with sums of 4 can be written as

n(A)=3
The probability that the sum of her rolls is 4 is given by
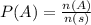
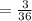
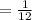
=0.083
∴ P(A)=0.083
∴ the probability that the sum of Michelle's rolls is 4 is 0.083