Question

A ladder 39 ft long leans against a vertical wall. If the lower end is being moved away from the wall at the rate of 4 ​ft/sec, how fast is the height of the top changing​ (this will be a negative​ rate) when the lower end is 15 feet from the​ wall?

Answer 1

The rate of change of height, dy / dt = -1.667 ft/s

Explanation:

Solution:-

- The length of the ladder, L = 39 ft

- The foot of the ladder is moved away from wall at a rate, dx/dt = 4ft/s

Find:-

how fast is the height of the top changing​ (this will be a negative​ rate) when the lower end is 15 feet from the​ wall?

Solution:-

- We will first draw a right angle triangle, with vertical height of the ladder to be"y" and distance of the foot of the ladder and the wall to be "x".

- Then express the length "L" in terms of x and y using pythagorean theorem:

L^2 = x^2 + y^2

y^2 = 39^2 - x^2

- Taking height of the ladder as the dependent variable and distance of the foot of the ladder from wall as independent variable.

- Formulate a differential equation from the given expression above in terms of "dy/dt" and "dx/dt". Perform implicit differential of the computed expression "d/dt":

2y*dy/dt = -2x*dx/dt

dy / dt = -(x/y)*dx/dt

- Where, dy / dt : The change in height of the ladder.

- The height of the ladder at x = 15 ft is:

`y = √(39^2 - x^2) = √(39^2 - 15^2) = 36`

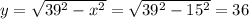
- Then evaluate dy/dt:

dy / dt = -(15/36)*4

dy / dt = -1.667 ft/s

Answer 2

-5/3 ft/sec

Explanation:

In this question, we are asked to calculate the rate at which the height of the top of a ladder is changing given that the lower end is being dragged at a particular rate.

Please check attachment for complete solution and step by step explanation.