Question

The average THC content of marijuana sold on the street is 10%. Suppose the THC content is normally distributed with standard deviation of 2%. Let X be the THC content for a randomly selected bag of marijuana that is sold on the street. Round all answers to two decimal places and give THC content in units of percent. For example, for a THC content of 11%, write "11" not 0.11.

Answer 1

(a)
`X\sim N(0.10,\ 0.02^(2))`.

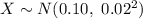(b) The probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 11% is 31%.

(c) The 60th percentile is 11%.

Explanation:

The complete question is:

The average THC content of marijuana sold on the street is 10%. Suppose the THC content is normally distributed with standard deviation of 2%. Let X be the THC content for a randomly selected bag of marijuana that is sold on the street. Round all answers to two decimal places and give THC content in units of percent. For example, for a THC content of 11%, write "11" not 0.11.

A. X ~ N( , )

B. Find the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 11%.

C.Find the 60th percentile for this distribution.

Solution:

The random variable X is defined as the THC content for a bag of marijuana that is sold on the street.

(a)

The random variable X is Normally distributed with mean, μ = 0.10 and standard deviation, σ = 0.02.

Thus,
`X\sim N(0.10,\ 0.02^(2))`.

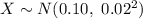(b)

Compute the value of P (X > 0.11) as follows:

`P(X>0.11)=P((X-\mu)/(\sigma)>(0.11-0.10)/(0.02))\\=P(Z>0.50)\\=1-P(Z<0.50)\\=1-0.69146\\=0.30854\\\approx 0.31`

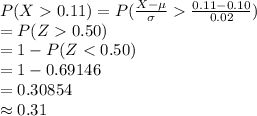
*Use a z-table.

Thus, the probability that a randomly selected bag of marijuana sold on the street will have a THC content greater than 11% is 31%.

(c)

The pth percentile is a data value such that at least p% of the data-set is less than or equal to this data value and at least (100 - p)% of the data-set are more than or equal to this data value.

Let x represent the 60th percentile value.

The, P (X < x) = 0.60.

⇒ P (Z < z) = 0.60

The value of z for this probability is,

z = 0.26.

Compute the value of x as follows:

`z=\farc{x-\mu}{\sigma}\\0.26=\farc{x-0.10}{0.02}\\x=0.10+(0.26* 0.02)\\x=0.1052\\x\approx 0.11`

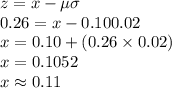
Thus, the 60th percentile is 11%.