Question

The interior angles of a hexagon are (2x+17)0, (3x - 25)0, (2x+49)0,

(x+40)0, (4x-17)0 and (3x - 4) 0.
i. Find the value of x.
ii. Find the smallest interior angle of the quadrilateral.
iii. Find the largest exterior angle of the quadrilateral.
iv. Find the largest exterior angle of the quadrilateral.

Answer 1

Answer: a) x= 68, b) 108°, c) 72°, d) 255°.

Explanation:

Since we have given that

The interior angles of hexagon:

(2x+17), (3x - 25), (2x+49), (x+40), (4x-17) and (3x - 4).

So, it becomes :

`2x+17+3x-25+2x+49+x+40+4x-17+3x-4=1080\\\\15x+60=1080\\\\15x=1080-60\\\\15x=1020\\\\x=68`

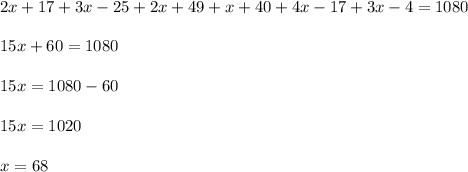
ii. Find the smallest interior angle of the quadrilateral.

`x+40=68+40=108^\circ`

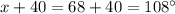
iii. Find the largest exterior angle of the quadrilateral.

`180-108=72^\circ`

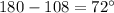
iv. Find the largest interior angle of the quadrilateral.

`4x-17=4* 68-17=255^\circ`

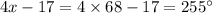
Hence, a) x= 68, b) 108°, c) 72°, d) 255°.