Question

Alice, Bob, and Charlotte are looking for butterflies. They look in three separate parts of a field, so that their probabilities of success do not affect each other. Alice finds 1 butterfly with probability 17%, and otherwise does not find one. Bob fines 1 butterfly with probability 25%, and otherwise does not find one. Charlotte finds 1 butterfly with probability 45%, and otherwise does not find one. Let X be the number of butterflies that they find together. What is the expected value of X?

Answer 1

The expected number of butterflies that they find together is 0.87.

Explanation:

Let A = number of butterflies caught by Alice, B = number of butterflies caught by Bob and C = number of butterflies caught by Charlotte.

The probability function of A is:

`A=\left \{ {{0.17;\ if\ A = 1} \atop {0.83;\ if\ A = 0}} \right.`

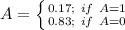
The probability function of B is:

`B=\left \{ {{0.25;\ if\ B = 1} \atop {0.75;\ if\ B = 0}} \right.`

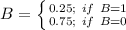
The probability function of C is:

`C=\left \{ {{0.45;\ if\ C = 1} \atop {0.55;\ if\ C = 0}} \right.`

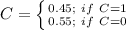
The random variable X is denoted as the number of butterflies that they find together.

Compute the expected value of X as follows:

E (X) = E (A + B + C)

= E (A) + E (B) + E (C)

`=[(0.17* 1)+(0.83* 0)]+[(0.25* 1)+(0.75* 0)]\\+[(0.45* 1)+(0.55* 0)]\\=0.17+0.25+0.45\\=0.87`

Thus, the expected number of butterflies that they find together is 0.87.