Answer:
Approximately
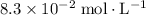 .
.
Step-by-step explanation:
The
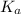 in this question refers the dissociation equilibrium of
in this question refers the dissociation equilibrium of
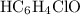 as an acid:
as an acid:
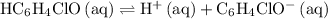 .
.
![\displaystyle K_a\left(\mathrm{HC_6H_4ClO}\right) = \frac{\left[\mathrm{H^(+)}\right] \cdot \left[\mathrm{C_6H_4ClO^(-)}\right]}{\left[\mathrm{HC_6H_4ClO}\right]}](https://img.qammunity.org/2021/formulas/chemistry/college/ep10fanntj2zdgp8vhki3buo9g2a8gp5hi.png) .
.
However, the question also states that the solution here has a
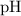 of
of
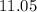 , which means that this solution is basic. In basic solutions at
, which means that this solution is basic. In basic solutions at
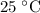 , the concentration of
, the concentration of
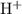 ions is considerably small (typically less than
ions is considerably small (typically less than
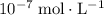 .) Therefore, it is likely not very appropriate to use an equilibrium involving the concentration of
.) Therefore, it is likely not very appropriate to use an equilibrium involving the concentration of
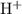 ions.
ions.
Here's the workaround: note that
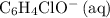 is the conjugate base of the weak acid
is the conjugate base of the weak acid
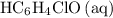 . Therefore, when
. Therefore, when
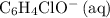 dissociates in water as a base, its
dissociates in water as a base, its
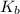 would be equal to
would be equal to
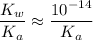 . (
. (
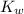 is the self-ionization constant of water.
is the self-ionization constant of water.
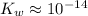 at
at
 .)
.)
In other words,
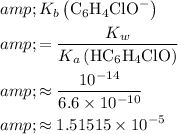 .
.
And that
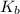 value corresponds to the equilibrium:
value corresponds to the equilibrium:
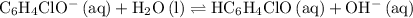 .
.
![\displaystyle K_b\left(\mathrm{C_6H_4ClO^(-)}\right) = \frac{\left[\mathrm{HC_6H_4ClO}\right]\cdot \left[\mathrm{OH^(-)}\right]}{\left[\mathrm{C_6H_4ClO^(-)}\right]}](https://img.qammunity.org/2021/formulas/chemistry/college/y5z4ojt72pvzbotb7hrh8i9sglkx1rod50.png) .
.
The value of
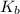 has already been found.
has already been found.
The
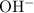 concentration of this solution can be found from its
concentration of this solution can be found from its
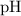 value:
value:
![\begin{aligned}& \left[\mathrm{OH^(-)}\right] \\ &= \frac{K_w}{\left[\mathrm{H}^(+)\right]} \\ & = \frac{K_w}{10^{-\mathrm{pH}}} \\ &\approx (10^(-14))/(10^(-11.05)) \\ &\approx 1.1220 * 10^(-3)\; \rm mol\cdot L^(-1) \end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/x915cyrt9byirj7vfqm4dfgww47v2zlvcv.png) .
.
To determine the concentration of
![\left[\mathrm{HC_6H_4ClO}\right]](https://img.qammunity.org/2021/formulas/chemistry/college/4z5hg1zgos5ldaygqw4038hhkrepaxh7p8.png) , consider the following table:
, consider the following table:
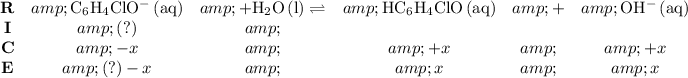
Before hydrolysis, the concentration of both
 and
and
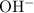 are approximately zero. Refer to the chemical equation. The coefficient of
are approximately zero. Refer to the chemical equation. The coefficient of
 and
and
 are the same. As a result, this equilibrium will produce
are the same. As a result, this equilibrium will produce
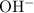 and
and
 at the exact same rate. Therefore, at equilibrium,
at the exact same rate. Therefore, at equilibrium,
![\left[\mathrm{HC_6H_4ClO}\right] \approx \left[\mathrm{OH^(-)}\right] \approx 1.1220 * 10^(-3)\; \rm mol\cdot L^(-1)](https://img.qammunity.org/2021/formulas/chemistry/college/lmwcjold3y815gfne7twr93scdqh0fbuao.png) .
.
Calculate the equilibrium concentration of
![\left[\mathrm{C_6H_4ClO^(-)}\right]](https://img.qammunity.org/2021/formulas/chemistry/college/dlvmzk6fhl0vojrrz6wijxma59vzx9mmfd.png) from
from
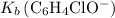 :
:
![\begin{aligned} & \left[\mathrm{C_6H_4ClO^(-)}\right] \\ &= \frac{\left[\mathrm{HC_6H_4ClO}\right]\cdot \left[\mathrm{OH^(-)}\right]}{K_b}\\&\approx (\left(1.1220 * 10^(-3)\right) * \left(1.1220 * 10^(-3)\right))/(1.51515* 10^(-5))\; \rm mol \cdot L^(-1) \\ &\approx 8.3 * 10^(-2)\; \rm mol \cdot L^(-1)\end{aligned}](https://img.qammunity.org/2021/formulas/chemistry/college/kahdet9zpfbrxvyn1ya7y37th08m5xzvcb.png) .
.