Question

Butterflies: • Alice, Bob, and Charlotte are looking for butterflies. They look in three separate parts of a field, so that their probabilities of success do not affect each other. • Alice finds 1 butterfly with probability 17%, and otherwise does not find one. • Bob finds 1 butterfly with probability 25%, and otherwise does not find one. • Charlotte finds 1 butterfly with probability 45%, and otherwise does not find one. Let X be the number of butterflies that they catch altogether. A) Find the expected value of X. B) Write X as the sum of three indicator random variables, X1,X2,X3 that indicate whether Alice, Bob, Charlotte (respectively) found a butterfly. Then X=X1+X2+X3. Find the expected value of X by finding the expected value of the sum of the indicator random variables.

Answer 1

The expected value is 0.87.

Explanation:

a) To calculate the expected value X we will first see the posible outcomes. So could take value of 0,1,2,3. We will calculate the probability of each outcome. To do so, we will introduce the following notation. Consider the following tuple (A,B,C) where A is the number of butterflies found by Alice, B the number found for by Bob and C the number found by C. To calculate the probability of the tuple (A,B,C) we will do as follows. If the entry of the tuple is 1, then we will multiply by the probability of the person that found the butterfly. So, if A =1, we will multiply by 0.17(Alice finds a butterfly with probability 0.17). On the other side, if the entry of the tuple is 0, we will multiply by (1-p) where p is the probability of the person that found the butterly. So, if A=0, we will multiply by 0.83. So, for example, consider the tuple (1,0,1). The probability of having this result is 0.17*0.75*0.45 (Alice and Charlotte found a butterfly, but Bob didn't). We can do this since we are said that their probabilities of success don't affect others' probabilities.

We will see the total number of butterflies and the tuples associated to that number. That is

X number of butterflies - tuples

0 butterflies - (0,0,0)

1 butterfly - (1,0,0) or (0,1,0) or (0,0,1)

2 butterflies - (1,1,0) or (1,0,1) or (0,1,1)

3 butterflies - (1,1,1)

To find the probability of the value of X, we will sum up the probability of the associated tuples. The values of the probabilities are as follows

(0, 0, 0) = 0.342375

(0, 0, 1 ) = 0.280125

(0, 1, 0) = 0.114125

(0, 1, 1 ) = 0.093375

(1, 0, 0) = 0.070125

(1, 0, 1 ) = 0.057375 = 0.17*0.75*0.45

(1, 1, 0) = 0.023375

(1, 1, 1) = 0.019125

In this case,

P(X=0) = 0.342375 ,

P(X=1) = 0.464375 = 0.280125 +0.114125+ 0.070125

P(X=2) = 0.174125

P(X =3 ) = 0.019125

So, the expected value of X is given by

0* 0.342375 +1 * 0.464375 +2* 0.174125+3*0.019125 = 0.87

b)Let X1 be the number of butterflies found by Alice, X2 the number found by Bob and X3 the number found by Charlotte. Then X = X1+X2+X3. Using the expected value properties and the independence of X1, X2 and X3 we have that E(X) = E(X1)+E(X2)+E(X3).

Recall that each variable is as follows. Xi is equal to 1 with probability p and it is 0 with probability (1-p). Then, the expected value of Xi is

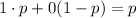`1\cdot p + 0\codt (1-p)=p`. Note that the value of p for X1,X2 and X3 is 17%, 25% and 45% respectively.

Then E(X) = 17%+25%+45%= 0.87.

So the expected number of butterflies is 0.87.