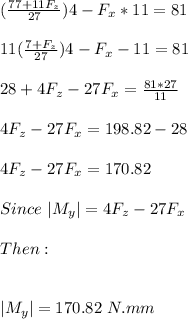Question

Can you solve it descriptively . thanks

static question
If the applied load F causes Mx
(-77 N.mm) and Mz
(-81 N.mm) at origin then
determine the My
at origin where d=27 mm

Answer 1

`|M_y| = 170.82 \ N.mm`

Step-by-step explanation:

From the diagram affixed below completes the question

Now from the diagram; We need to resolve the force at point A into (3) components ; i.e x.y. & z directions which are equivalent to
`F_x \ , F_y \ , F_z`

So;

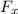`F_x` = positive x axis

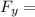`F_y =` Negative y axis

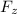`F_z` = positive z axis

Then;

`|M_x| = F_y *27-F_z*11 = 77 ----- equation(1) \\ \\ |M_z| = F_y*4 - F_x*11 = 81 ---- equation (2) \\ \\ |M_y| = F_x *27 - F_z *4 = ? ---- equation (3)`

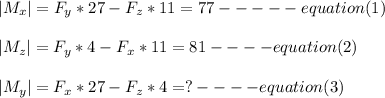
From equation (1); Let's make
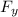`F_y` the subject of the formula ; then :

`F_y = (77+11F_z)/(27)`

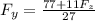
Substituting the value for
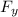`F_y` into equation (2) ; we have:

`((77+11F_z)/(27))4-F_x*11=81 \\ \\ 11((7+F_z)/(27) ) 4- F_x -11 =81 \\ \\ 28+4 F_z - 27F_x = (81*27)/(11) \\ \\ 4F_z - 27F_x = 198.82 -28 \\ \\ 4F_z - 27F_x = 170.82 \\ \\ Since \ |M_y| = 4F_z-27F_x \\ \\ Then: \\ \\ \\ |M_y| = 170.82 \ N.mm`