Answer:
The area of the rectangular area is (1400w-w²) square yards.
Explanation:
Given that,
David has available 2800 yards of fencing. He wants to enclose a rectangular area.
Assume that, the length and width of the rectangular be l and w respectively.
The perimeter of the rectangular area is
=2(length+ width)
=2(l+w)
So,
2(l+w)= 2800
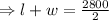
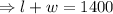
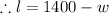
The area of the rectangular area is = length× width
=l×w
=(1400-w) w
=(1400w-w²) square yards.