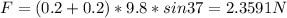Answer:
Incomplete question: "Each block has a mass of 0.2 kg"
The speed of the two-block system's center of mass just before the blocks collide is 2.9489 m/s
Step-by-step explanation:
Given data:
θ = angle of the surface = 37°
m = mass of each block = 0.2 kg
v = speed = 0.35 m/s
t = time to collision = 0.5 s
Question: What is the speed of the two-block system's center of mass just before the blocks collide, vf = ?
Change in momentum:
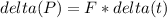
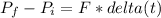
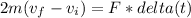

It is neccesary calculate the force:
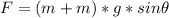
Here, g = gravity = 9.8 m/s²