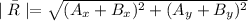Note: You did not provide the the diagram you referred to but i will explain how to find the magnitude of the resultant of two vectors, you can then put your own values whenever you have them.
Answer:
For any,
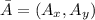 , and
, and
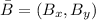 , the magnitude of the resultant will be
, the magnitude of the resultant will be
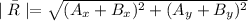
Explanation:
The resultant of two vectors
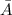 and
and
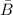 is the addition of the two vectors
is the addition of the two vectors
I.e.

If
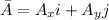 and
and
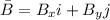 , then
, then

The magnitude of the Resultant will then be :