Question

Please Help

The surface area S of a cube is equal to the sum of the areas of the 6 square faces that form the cube. We want to paint the cube and need to know how many square units of paint to purchase. If each face has side length s, then the formula S = 6s2 can be used to find the surface area of the cube. The length of a side is indicated in the cube below( s = x - 5). The surface area of the cube is 1944 units2.

What is the value of x? SHOW and EXPLAIN each of the steps you used to solve

Answer 1

23

Explanation:

-The length of the cubes side is (x-5) and the total surface area is 1944 sq units.

-We apply the formula for surface area and equate to solve for x:

`A=6s^2\\\\1944=6(x-5)^2\\\\324=(x-5)^2\\\\324=x^2-10x+25`

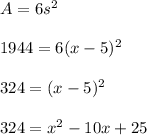
#Equate to zero as below:

`324=x^2-10x+25\\\\x^2-10x+25-324=0\\\\x^2-10x-299=0\\\\\# Quadratic \ Formula:\\\\x_(1,2)=(-b\pm √(b^2-4ac))/(2a)\\\\\\=(10\pm√((-10)^2-4(1*-299)))/(2*1)\\\\x_1=23, \ \ \ x_2=-13`

length dimensions are always positive.

Hence, the value of x is 23