Question

Elasticity of Demand The demand function for a certain brand of backpacks is

P=50 ln(50/x)
where P is the unit price in dollars and X is the quantity (in hundreds) demanded per month.


1) Find the elasticity of demand, and determine the range of prices corresponding to inelastic, unitary, and elastic demand.

2) If the unit price is increased slightly from $50, will the revenue increase or decrease?

Answer 1

See explanation

Explanation:

Solution:-

- The demand function of a certain brand is given as price P a function of x quantity of goods ( in hundred ) demanded per month. The relation is:

P ( x ) = 50 Ln ( 50 / x ).

- The point price elasticity ( E ) of demand is given by:

`E = (P)/(x)*(dP)/(dx)`

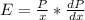
- Where, dP / dx : is the rate of change of price ( P ) with each hundred unit of good ( x ) is demanded.

- To determine the " dP / dx " by taking the first derivative of the given relation:

P ( x ) = 50 Ln ( 50 / x ).

d P ( x ) / dx = [ 50*x / 50 ] * [ -1*50 / x^2 ]

= - 50 / x

- Hence the point price elasticity of demand is given by:

E = - ( P / x ) * ( 50 / x )

E = -50*P / x^2

- For an inelastic demand, ! E ! is < 1:

! -50*P / x^2 ! < 1

50*P / x^2 < 1

P < x^2 / 50

- For an unitary demand, ! E ! is = 1:

! -50*P / x^2 ! = 1

50*P / x^2 = 1

P = x^2 / 50

- For an inelastic demand, ! E ! is > 1:

! -50*P / x^2 ! > 1

50*P / x^2 > 1

P > x^2 / 50

2)

If the unit price is increased slightly from $50, will the revenue increase or decrease?

- We see from the calculated demand sensitivity d P / dt:

d P ( x ) / dx = - 50 / x

- We see that as P increases the from P = $50, the quantity of goods demanded would be:

50 = 50 ln(50/x)

1 = Ln ( 50 / x )

50/x = e

x = 50 / e

Then,

d P ( x ) / dx = - 50 / ( 50 / e )

d P ( x ) / dx = - e

- We see that if price slightly increases from $ 50 then the quantity demanded would decrease by e (hundreds ) goods.

- The decrease in the quantity demanded is higher than the increase in price. The revenue is given by the product of price P ( x ) and x:

Revenue R ( x ) = P ( x ) * x

= 50*x*ln(50/x)

Then the product of price and quantity goods also decreases; hence, revenue decreases.