Question

A certain chemical pollutant in the Arkansas River has been constant for several years with mean μ = 34 ppm (parts per million). A group of factory representatives whose companies discharge liquids into the river is now claiming they have lowered the average with improved filtration devices. A group of environmentalists will test to see if this is true. Find the rejection region appropriate for this test if we are using a significance level of 0.05 and have a sample size of 25.

A) Reject H0 if t < -1.960

B) Reject H0 if t < -2.064

C) Reject H0 if t < -1.711

D) Reject H0 if t < -1.708

E) Reject H0 if t < -2.064 or t > 2.064

Answer 1

C) Reject
`H_0` if t < -1.711

Explanation:

We are given that a certain chemical pollutant in the Arkansas River has been constant for several years with mean μ = 34 ppm (parts per million).

Also, it is given that the level of significance is 0.05 and a sample size of 25 is taken.

Let
`\mu` = average chemical pollutant in the Arkansas River

So, Null Hypothesis,
`H_0` :
`\mu` = 24 ppm {means that the average is same as before with improved filtration devices}

Alternate Hypothesis,
`H_A` :
`\mu` < 24 ppm {means that they have lowered the average with improved filtration devices}

Now, t test statistics is given by; T.S. =
`(\bar X -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

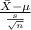where, n = sample size = 25

n - 1 = degree of freedom = 25 - 1 = 24

Now, at 0.05 significance level in the t table, the critical value at 24 degree of freedom is given as - 1.711 for left tailed test.

So, we will reject our null hypothesis when the t test statistics is less than the critical value of t which means reject null hypothesis if t < -1.711.