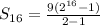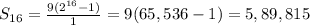Answer:
The sum of the first 16 terms of the geometric sequence
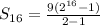
S₁₆ = 5,89,815
Step-by-step explanation:
Step-by-step explanation:-
Geometric series:-
The geometric sequence has its sequence Formation
a , a r, ar² , ar³,...…..a rⁿ be the n t h sequence
Given first term a=9 and common ratio 'r' = 2
The sum of the first 16 terms of the geometric sequence
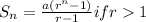
Given first term a=9 , 'r' = 2 and n=16