Question

In the survey of 891 US adults who follow baseball in a recent year, 184 said that the Boston red sox would win the world series. Construct a 90% confidence interval for the population proportion of US adults who follow baseball who in a recent year said the Boston red sox would win the world series

Answer 1

90% confidence interval for the population proportion of US adults who follow baseball

( 0.1842 , 0.22880)

Explanation:

Explanation:-

Given data the survey of 891 US adults who follow baseball in a recent year, 184 said that the Boston red sox would win the world series.

The sample proportion
`'p' = (184)/(891) = 0.20650`

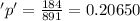
q = 1-p = 1- 0.20650 =0.79350

Confidence intervals

90% confidence interval for the population proportion of US adults who follow baseball

`(p-Z_(\alpha ) \sqrt{(pq)/(n) } , p + Z_(\alpha ) \sqrt{(pq)/(n) } )`

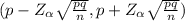
The tabulated value Z₀.₉₀ = 1.645

`(0.20650-1.645\sqrt{(0.20650X0.7935)/(891) } , 0.20650 + 1.645\sqrt{(0.20650X0.7935)/(891) } )`

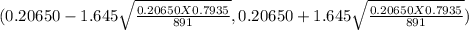
(0.20650 - 0.02230 , 0.20650+0.02230)

( 0.1842 , 0.22880)

Conclusion:-

90% confidence interval for the population proportion of US adults who follow baseball

( 0.1842 , 0.22880)