Question

Can someone help with this

Answer 1

Hi there!

A.

We can use the work-energy theorem to solve.

Initially, both blocks have gravitational potential energy, which is then converted to kinetic energy.

Recall:

`U = mgh \\`

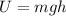
U = Potential Energy (J)
m = mass (kg)
g = acceleration due to gravity (m/s²)

h = height (m)

And at the end, block 2 has both kinetic and potential energy. Kinetic is defined as:

`KE = (1)/(2)mv^2`

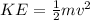
v = velocity (m/s)

We can do a summation of initial and final forces.

Initial:

`E_i = m_2g(h)/(2) + m_1gh`

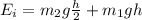
Final:

`E_f = (1)/(2)m_2 v^2 + m_2g(3h)/(2) + (1)/(2)m_1 v^2`

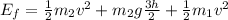
Set the two equal (no energy loss in this situation) and solve for velocity.

`m_2g(h)/(2) + m_1gh = (1)/(2)m_2 v^2 + m_2g(3h)/(2) + (1)/(2)m_1 v^2\\\\m_2g(h)/(2) + m_1gh - m_2g(3h)/(2) = (1)/(2)m_2 v^2 + (1)/(2)m_1 v^2\\\\v^2 = (gh((m_2)/(2) + m_1 - (3m_2)/(2)))/((1)/(2)m_2 + (1)/(2)m_1)\\\\v = \sqrt{(gh((m_2)/(2) + m_1 - (3m_2)/(2)))/((1)/(2)m_2 + (1)/(2)m_1)}\\\\v = \boxed{3.704 (m)/(s)}`

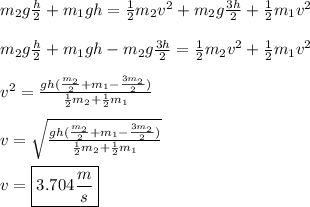
**This can be solved in a simpler way using a summation of forces.

B.

Now, we can do a summation of forces to solve. First, we must solve for the acceleration of the system now that we have found the velocity. Use the kinematic equation:

`v_f^2 = v_i^2 + 2ad`

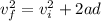
Initial velocity is 0 m/s, so:

`v_f^2 = 2ad\\\\a = (v_f^2)/(2d) = ((3.704^2))/(2(2.10)) = 3.267 (m)/(s^2)`

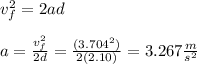
Now, we can use a summation of forces for any block. We can do block 1:

`\Sigma F = m_1g - T`

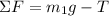
Using Newton's Second Law:

`m_1a = m_1g - T\\\\T = m_1g - m_1a \\T = m_1 (g - a) = 4.10(9.8 - 3.267) = \boxed{26.828 N}`