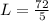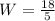Question

The length of a rectangle is 4 times its width.

The perimeter is 36.
Find the length and width of the rectangle.

Answer 1

Length=14.4

Width=3.6

Explanation:

l=4w

2l+2w=36

2(4w)+2w=36

8w+2w=36

10w=36

w=3.6

l=4w

4(3.6)

l=14.4

*check by plugging in answers into 2l+2w=36*

Answer 2

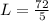`L=(72)/(5)` or 14.4

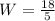`W=(18)/(5)` or 3.6

Explanation:

Please take note this probably not the easiest way to do the problem.

Formula for the Perimeter of Rectangle

`P=2L+2W`

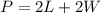
We are given the perimter.

`36=2L+2W`

`L=4*W`

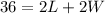
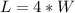
To solve I would use the Gauss-Jordan method. (it is advanced, but it makes sense to me)

`36=2L+2W`

`L=4*W`

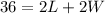
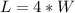
Write the coefficients of each eqaution as rows in the matrix.

`\left[\begin{array}{ccc}2&2&36\\1&-4&0\\\end{array}\right]`

Divide the first row by 2.

`\left[\begin{array}{ccc}1&1&18\\1&-4&0\\\end{array}\right]`

Multiply row 1 by -1 and add it to row 2.

`\left[\begin{array}{ccc}1&1&18\\0&-5&-18\\\end{array}\right]`

Divide the second row by -5.

`\left[\begin{array}{ccc}1&1&18\\0&1&(18)/(5) \\\end{array}\right]`

Multiply row 2 by -1 and add it to row 1.

`\left[\begin{array}{ccc}1&0&(72)/(5) \\0&1&(18)/(5) \\\end{array}\right]`

We now have an augmented matrix.

`L=(72)/(5)`

`W=(18)/(5)`