Before we solve this problem:
⇒ let's figure out what all the variables in the equation stand for
- t: number of years after initial rabbit population
- r(t): number rabbits in 't' years
Question 16: How many rabbits will there be in 8 years?
- Since it is asking how many rabbits there be in 8 years
⇒ that means we substitute 8 into 't' of the equation
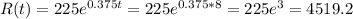
*we will round down the number of rabbits since it is impossible to
have 0.2 of a rabbit
There will be 4519 rabbits in 8 years.
Question 17: When will the population be 15000?
- Since it asking for when the population or R(t) will be 15000
⇒ we substitute 15000 into 'R(t)' of the function and solve for 't'
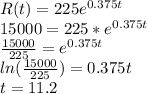
*in this case, you want it to the nearest year, round it up since we
asked for how many years, and if we were to say 11, the
the population of rabbits wouldn't have reached that number yet,
so we will round up to ensure that number has been reached by
that year.
It will take at least 12 years for the rabbit population to reach 15000
Hope that helps!