Question

A 0.100-kg ball traveling horizontally on a frictionless surface approaches a very massive stone at 20.0 m/s perpendicular to wall and rebounds with 70.0% of its initial kinetic energy. What is the magnitude of the change in momentum of the stone

Answer 1

Change in momentum of the stone is 3.673 kg.m/s.

Step-by-step explanation:

Given:

Mass of the ball on the horizontal the surface, m = 0.10 kg

Velocity of the ball with which it hits the stone, v = 20 m/s

According to the question it rebounds with 70% of the initial kinetic energy.

We have to find the change in momentum i.e Δp

Before that:

We have to calculate the rebound velocity with which the object rebounds.

Lets say that the rebound velocity be "v1" and KE remaining after the object rebounds be "KE1".

⇒
`KE_1=0.7* (mv^2)/(2)`

⇒
`KE_1=0.7* (0.10* (20)^2)/(2)`

⇒
`KE_1=0.7* (0.10* 400)/(2)`

⇒
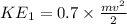
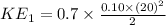
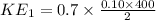
`KE_1=14` Joules (J).

Rebound velocity "v1".

⇒
`KE_1=(m(v_1)^2)/(2)`

⇒
`v_1 = \sqrt{(2KE_1)/(m) }`

⇒
`v_1 = \sqrt{(2* 14)/(0.10) }`

⇒
`v_1=16.73`

⇒
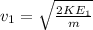
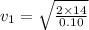
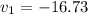`v_1=-16.73` m/s ...as it rebounds.

Change in momentum Δp.

⇒
`\triangle p= m\triangle v`

⇒
`\triangle p= 0.10* (20-(-16.73)`

⇒
`\triangle p= 0.10* (20+16.73)`

⇒
`\triangle p= 0.10* (36.73)`

⇒
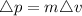
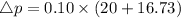
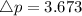`\triangle p = 3.673` Kg.m/s

The magnitude of the change in momentum of the stone is 3.673 kg.m/s.