Question

g Using the complex based titration system: 50.00 mL 0.00250 M Ca2 titrated with 0.0050 M EDTA, buffered at pH 11.0 determine (i) first pCa first before initiating the titration process and then (ii) at equivalence when all the Ca2 is titrated to CaY2-. Please, use your text books and/or lecture notes to find potentially missing information about constants needed to solve the problem.

Answer 1

Step-by-step explanation:

a).

conc of Ca²⁺ =0.0025 M

pCa = -log(0.0025) = 2.6

logK,= 10.65 So lc = 4.47 x 10.

Formation constant of Ca(EDTA)]-z= 4.47 x 10¹⁰ At pH = 11, the fraction of EDTA that exists Y⁻⁴ is
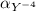`\alpha_(Y^(-4))` =0.81

So the Conditional Formation constant=
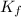`K_f` =0.81x 4.47 x10¹⁰

=3.62x10¹⁰

b)

At Equivalence point:

Ca²⁺ forms 1:1 complex with EDTA At equivalence point,

Number of moles of Ca²⁺= Number of moles of EDTA Number of moles of Ca²⁺ = M×V = 0.00250 M × 50.00 mL = 0.125 mol

Number of moles of EDTA= 0.125 mol

Volume of EDTA required = moles/Molarity = 0.125 mol / 0.0050 M = 25.00 mL

V e= 25.00 mL

At equivalence point, all Ca²⁺ is converted to [CaY²⁻] complex. So the concentration of Ca²⁺ is determined by the dissociation of [CaY²⁻] complex.

`[CaY^(2-)] = (Initial,moles,of, Ca^(2+))/(Total,Volume) = (0.125mol)/((50.00+25.00)mL) = 0.001667M`

`{K^'}_f`

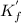
Ca²⁺ + Y⁴ ⇄ CaY²⁻

Initial 0 0 0.001667

change +x +x -x

equilibrium x x 0.001667 - x

`{K^'}_f = ([CaY^(2-)])/([Ca^(2+)][Y^4])=(0.001667-x)/(x.x) =(0.001667-x)/(x^2)\\\\x^2 = \frac{0.001667-x}{{K^'}_f}\\ \\`

`x^2=(0.001667)/(3.62*10^(10))=4.61\exp-14`

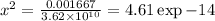
x = 2.15×10⁻⁷

[Ca+2] = 2.15x10⁻⁷ M

pca = —log(2 15x101= 6.7