Question

What polynomial has quotient x2 + 6x – 4 when divided by x + 3?​

Answer 1

`(x^(3) + 9\, x^(2) + 14\, x - 12)`.

Explanation:

Let
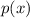`p(x)` denote the polynomial in question.

The question states that dividing
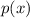`p(x)` by
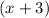`(x + 3)` gives the quotient
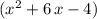`(x^(2) + 6\, x - 4)` (with no remainder.) In other words:

`\displaystyle (p(x))/(x + 3) = x^(2) + 6\, x - 4`.

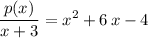Multiply both sides by
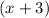`(x + 3)` to find an expression for the polynomial in question,
`p(x)`:

`p(x) = (x^(2) + 6\, x - 4)\, (x + 3)`.

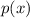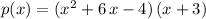Expand this expression to obtain:

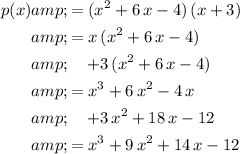`\begin{aligned}p(x) &= (x^(2) + 6\, x - 4) \, (x + 3) \\ &= x\, (x^(2) + 6\, x - 4) \\ & \quad + 3\, (x^(2) + 6\, x - 4) \\ &= x^(3) + 6\, x^(2) - 4\, x \\ &\quad + 3\, x^(2) + 18\, x - 12 \\ &= x^(3) + 9\, x^(2) + 14\, x - 12\end{aligned}`.