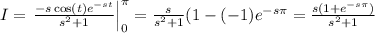Answer:
The laplace transform is
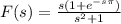
Explanation:
Let us asume that f(t) =0 for t<0. So, by definition, the laplace transform is given by:
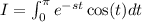
To solve this integral, we will use integration by parts. Let u= cos(t) and dv =
 , so v=
, so v=
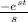 and du = -sin(t), then, in one step of the integration we have that
and du = -sin(t), then, in one step of the integration we have that
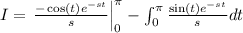
Let
 . We will integrate I_2 again by parts. Choose u = sin(t) and dv =
. We will integrate I_2 again by parts. Choose u = sin(t) and dv =
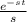 . So
. So
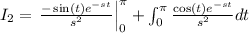
Therefore,
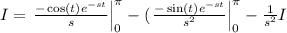
which is an equation for the variabl I. Solving for I we have that
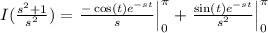
Then,
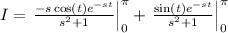 .
.
Note that since the sine function is 0 at 0 and pi, we must only care on the first term. Then