Question

Exercise 11.21) Many smartphones, especially those of the LTE-enabled persuasion, have earned a bad rap for exceptionally bad battery life. Battery life between charges for the Motorola Droid Razr Max averages 20 hours when the primary use is talk time and 7 hours when the primary use is Internet applications (The Wall Street Journai, March 7, 2012). Since the mean hours for talk time usage is greater than the mean hours for Internet usage, the question was raised as to whether the variance in hours of usage is also greater when the primary use is talk time. Sample data showing battery hours of use for the two applications follows. Click on the datafile logo to reference the data DATAfile Primary Use: Talking 35.8 8.0 22.2 3.8 4.0 30.0 32.6 12.8 8.5 10.3 42.5 35.5 Primary Use: Internet 14.0 5.4 16.4 15.2 9.9 4.7 12.5 4.0 a. Formulate hypotheses about the two population variances that can be used to determine if the population variance in battery hours of use is greater for the talk time application. 0: σ' less than or equal to σ2 ia: σ12 greater than b. What are the standard deviations of battery hours of use for the two samples? Round your answers to two decimal places. S114.13 $2=| 5.76 c. Conduct the hypothesis test and compute the p-value. Round your answers to three decimal places.

Answer 1

Explanation:

Hello!

The researcher suspects that the battery life between charges for the Motorola Droid Razr Max differs if its primary use is talking or if its primary use is for internet applications.

Since the means for talk time usage (20hs) is greater than the mean for internet usage (7hs) the main question is if the variance in hours of usage is also greater when the primary use is talk time.

Be:

X₁: Battery duration between charges when the primary usage of the phone is talking. (hs)

n₁= 12

X[bar]₁= 20.50 hs

S₁²= 199.76hs² (S₁= 14.13hs)

X₂: Battery duration between charges when the primary usage of the phone is internet applications.

n₂= 10

X[bar]₂= 8.50

S₂²= 33.29hs² (S₂= 5.77hs)

Assuming that both variables have a normal distribution X₁~N(μ₁;σ₁²) and X₂~N(μ₂; σ₂²)

The parameters of interest are σ₁² and σ₂²

a) They want to test if the population variance of the duration time of the battery when the primary usage is for talking is greater than the population variance of the duration time of the battery when the primary usage is for internet applications. Symbolically: σ₁² > σ₂² or since the test to do is a variance ratio: σ₁²/σ₂² > 1

The hypotheses are:

H₀: σ₁²/σ₂² ≤ 1

H₁: σ₁²/σ₂² > 1

There is no level of significance listed so I've chosen α: 0.05

b) I've already calculated the sample standard deviations using a software, just in case I'll show you how to calculate them by hand:

S²=
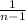`(1)/(n-1)`*[∑X²-(∑X)²/n]

For the first sample:

n₁= 12; ∑X₁= 246; ∑X₁²= 7240.36

S₁²=
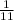`(1)/(11)`*[7240.36-(246)²/12]= 199.76hs²

S₁=√S₁²=√199.76= 14.1336 ≅ 14.13hs

For the second sample:

n₂= 10; ∑X₂= 85; ∑X₂²= 1022.12

S₂²=
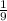`(1)/(9)`*[1022.12-(85)²/10]= 33.2911hs²

S₂=√S₂²=√33.2911= 5.7698 ≅ 5.77hs

c)

For this hypothesis test, the statistic to use is a Snedecors F:

`F= (S_1^2)/(S_2^2) *(Sigma_1^2)/(Sigma_2^2) ~~F_(n_1-1;n_2-1)`

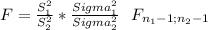
This test is one-tailed right, wich means that you'll reject the null hypothesis to big values of F:

`F_(n_1-1;n_2-1; 1-\alpha )= F_(11;9;0.95)= 3.10`

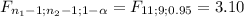
The rejection region is then F ≥ 3.10

`F_(H_0)= (199.76)/(33.29) * 1= 6.0006`

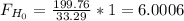
p-value: 0.006

Considering that the p-value is less than the level of significance, the decision is to reject the null hypothesis.

Then at a 5% level, there is significant evidence to conclude that the population variance of the duration time of the batteries of Motorola Droid Razr Max smartphones used primary for talk is greater than the population variance of the duration time of the batteries of Motorola Droid Razr Max smartphones used primary for internet applications.

I hope this helps!