Question

In the United States, 36 percent of the people have a blood type that is A positive. From a random sample of 150 people from Norway, 66 had a blood type that was A positive. Consider a hypothesis test to investigate whether the proportion of people in Norway with a blood type of A positive is different from that in the United States. Which of the following is the standard deviation used to calculate the test statistic for the one-sample z-test? (0.24) (0.76) 150 (0.44) (0.56) 150 (0.36)(0.64) 150 (0.44)(0.56) 150 (0.36 (0.64) 150

Answer 1

The standard deviation used to calculate the test statistic for the one-sample z-test is 0.04.

Explanation:

A single proportion z-test can be performed to determine whether the proportion of people in Norway with a blood type of A positive is different from that in the United States.

It is provided that the percentage of people in the US with blood type A positive is, p = 36%.

A random sample of n = 150 people from Norway are selected to check the above claim.

The hypothesis can be defined as:

H₀: The proportion of people in Norway with a blood type of A positive is same as that in the United States, i.e. p = 0.36.

Hₐ: The proportion of people in Norway with a blood type of A positive is different from that in the United States, i.e. p ≠ 0.36.

The test statistic for the the hypothesis testing is:

`z=(\hat p-\mu_(\hat p))/(\sigma_(\hat p))`

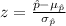
The mean of the sample proportion is:

`\mu_(\hat p)=p`

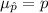
The standard deviation of sample proportion is:

`\sigma_(\hat p)=\sqrt{(p(1-p))/(n)}`

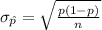
Compute the standard deviation value as follows:

`\sigma_(\hat p)=\sqrt{(p(1-p))/(n)}`

`=\sqrt{(0.36(1-0.36))/(150)}`

`=0.03919184\\\approx0.04`

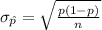
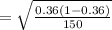
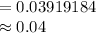
Thus, the standard deviation used to calculate the test statistic for the one-sample z-test is 0.04.