Question

A fence is to be built to enclose a rectangular area of 450450 square feet. The fence along three sides is to be made of material that costs ​$33 per foot. The material for the fourth side costs ​$99 per foot. Find the dimensions of the rectangle that will allow for the most economical fence to be built.

Answer 1

The dimensions of the rectangle that will allow for the most economical fence to be built are 30x15 feets, where two sides of 30 feets long cost $33 each one per foot, one side of 15 feets costs also $33 and the remaining side costs $99

Explanation:

If x and y were the dimensions of the rectangle (in feets), then we have that x*y = 450. Therefore, y = 450/x.

Note that the rectangle as a result is formed by 2 sides with length x and 2 other sides with length 450/x. Lets suppose that x is the length of the 2 sides that costs both $33 and the other two sides, which have length 450/x, one costs also $33 and the other costs $99.

The cost, in $, function f,in terms of x, is given as follows

`f(x) = 2 * 33 * x + 33*(450)/(x) + 99*(450)/(x) = 66x + (59400)/(x)`

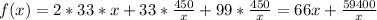
We want to minimize f, so we will derivate it and equalize the derivate to 0:

`f'(x) = 66 - (59400)/(x^2)`

`f'(x) = 0 \leftrightarrow 66 = (59400)/(x^2) \leftrightarrow x^2 = (59400)/(66) = 900 \leftrightarrow x = √(900) = 30`

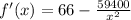
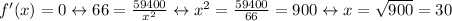
(Note that x cant be negative, so in the equation we didnt count the opposite of the square root of 900)

We concluded that one dimension is 30 feets, and the other should be 450/30 = 15.