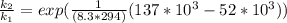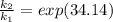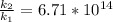Question

Since changing the environment of the spill is not possible, you need other ways to speed up oil decomposition. One method is to add a biological catalyst, an enzyme mixture known as Oil Spill Eater. As a catalyst, Oil Spill Eater reduces the activation energy of oil decomposition from 137. kJ/mol to 52.0 kJ/mol. By what factor would you expect the rate constant to increase at 27°C?

Answer 1

The factor by which the rate constant increases is
`(k_2)/(k_1) = 6.71 *10^(14)`

Step-by-step explanation:

From the question we are told that

The activation energy of oil before addition of Oil Spill Easter

`E_a_1 = 137.kJ/mol`

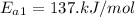
The activation energy of oil after addition of Oil Spill Easter

`E_a_2 = 52.0 kJ/mol`

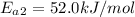
The temperature is
`T = 27^o C`

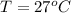
The objective of this solution is to obtain the factor by which the rate constant increase at 27°C

This can be obtained using the Arrhenius equation

This equation is mathematically represented as

`k = A exp ((-E_a)/(R T) )`

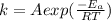
Where A is the frequency

k is the rate constant

R is the gas constant

This Arrhenius equation show a relationship between rate of reaction and

Activation energy

The decomposition of oil without catalyst is expressed as

`k_1 = A exp ( (-E_a_1)/(RT) )`

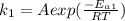
The decomposition of oil with catalyst is expressed as

`k_1 = A exp ( (-E_a_2)/(RT) )`

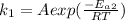
Now dividing
`k_2 \ by \ k_1`

`(k_2)/(k_1) = (A exp ((-E_a_2)/(RT) ))/(A exp ((-E_a)/(RT) ) )`

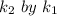
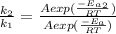
applying rule of exponent

`(k_2)/(k_1) = exp ((-E_a_2)/(RT) + (E_a_1)/(RT) )`

`(k_2)/(k_1) = exp((1)/(RT) (E_a_1 - E_a_2) )`

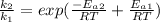
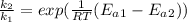
Substituting value

`(k_2)/(k_1) = exp ((1)/((8.3 * 294)) (137 * 10^3 - 52 * 10^(3)) )`

`(k_2)/(k_1) = exp(34.14)`

`(k_2)/(k_1) = 6.71 *10^(14)`