Question

To view an interactive solution to a problem that is similar to this one, select Interactive Solution 7.24. A 0.0129-kg bullet is fired straight up at a falling wooden block that has a mass of 1.17 kg. The bullet has a speed of 767 m/s when it strikes the block. The block originally was dropped from rest from the top of a building and had been falling for a time t when the collision with the bullet occurs. As a result of the collision, the block (with the bullet in it) reverses direction, rises, and comes to a momentary halt at the top of the building. Find the time t.

Answer 1

t=0.42s

Step-by-step explanation:

Here you have an inelastic collision. By the conservation of the momentum you have:

`m_1v_1+m_2v_2=(m_1+m_2)v`

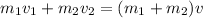
m1: mass of the bullet

m2: wooden block mass

v1: velocity of the bullet

v2: velocity of the wooden block

v: velocity of bullet and wooden block after the collision.

By noticing that after the collision, both objects reach the same height from where the wooden block was dropped, you can assume that v is equal to the negative of v2. In other words:

`m_1(-v_1)+m_2v_2=(m1+m2)(-v2)`

Where you assumed that the negative direction is upward. By replacing and doing v2 the subject of the formula you get:

`-(0.0129kg)(767m/s)+(1.17kg)v_2=(1.1829kg)(-v_2)\\\\v_2=4.20m/s`

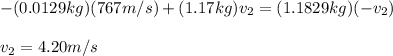
Now, with this information you can use the equation for the final speed of an accelerated motion and doing t the subject of the formula. IN other words:

`v_2=v_o+gt\\\\t=(v_2-v_o)/(g)=(4.2m/s-0m/s)/(9.8m/s^2)=0.42s`

hence, the time is t=0.42 s