Question

German physicist Werner Heisenberg related the uncertainty of an object's position ( Δ x ) to the uncertainty in its velocity ( Δ v ) Δ x ≥ h 4 π m Δ v where h is Planck's constant and m is the mass of the object. The mass of an electron is 9.11 × 10 − 31 kg. What is the uncertainty in the position of an electron moving at 1.00 × 10 6 m/s with an uncertainty of Δ v = 0.01 × 10 6 m/s ?

Answer 1

The uncertainty in the position of the electron is
`5.79x10^(-9)m`

Step-by-step explanation:

The Heisenberg uncertainty principle is defined as:

`\Lambda p\Lambda x` ≥
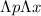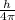`(h)/(4 \pi)` (1)

Where
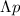`\Lambda p` is the uncertainty in momentum,
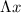`\Lambda x` is the uncertainty in position and h is the Planck's constant.

The momentum is defined as:

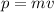`p =mv` (2)

Therefore, equation 2 can be replaced in equation 1

`\Lambda (mv) \Lambda x` ≥
`(h)/(4 \pi)`

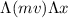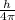
Since, the mass of the electron is constant, v will be the one with an associated uncertainty.

`m \Lambda v \Lambda x` ≥
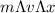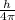`(h)/(4 \pi)` (3)

Then,
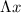`\Lambda x` can be isolated from equation 3

`\Lambda x` ≥
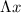`(h)/(m \Lambda v 4 \pi)` (4)

`\Lambda x = (6.626x10^(-34)J.s)/((9.11x10^(-31) kg)(0.01x10^(6)m/s) 4 \pi)`

But
`1J = Kg.m^(2)/s^(2)`

`\Lambda x = ((6.624x10^(-34) Kg.m^(2)/s^(2).s))/((9.11x10^(-31) kg)(0.01x10^(6)m/s) (4 \pi))`

`\Lambda x = 5.79x10^(-9)m`

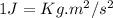
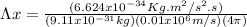
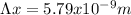
Hence, the uncertainty in the position of the electron is
`5.79x10^(-9)m`