Answer:
The mass of the wheel is 2159.045 kg
Step-by-step explanation:
Given:
Radius
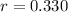
m
Force
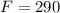 N
N
Angular acceleration
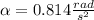
From the formula of torque,
Γ
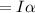 (1)
(1)
Γ
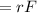 (2)
(2)
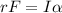
Find momentum of inertia
 from above equation,
from above equation,

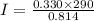
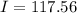
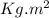
Find the momentum inertia of disk,
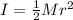

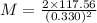
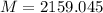 Kg
Kg
Therefore, the mass of the wheel is 2159.045 kg