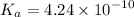Question

A 0.563 M solution of the salt NaA has a pH of 11.56. Calculate the Ka value for the acid HA. Record your answer in scientific notation to 3 sig figs.

Answer 1

`\displaystyle K_a = 4.24* 10^(-10)`

Step-by-step explanation:

Write the base reaction of NaA with water:

`\displaystyle \text{A}^-_\text{(aq)}+\text{H$_2$O}_\text{($\ell$)}\rightleftharpoons \text{HA}_\text{(aq)} + \text{OH}^-_\text{(aq)}`

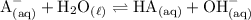
Hence, the equilibrium constant expression for the reaction is:

`\displaystyle K_b = \frac{[\text{OH}^-][\text{HA}]}{[\text{A}^-]}`

Thus, to find Ka, we can find Kb and use the fact that Ka × Kb = Kw.

From the reaction and initial concentration of NaA, create an ICE chart:

`\begin{tabular}{llllll} & A^- &\text{H$_2$O} & \rightleftharpoons & HA & OH^- \\I & 0.563 M & \---- & & 0 M & 0 M \\C & -\text{ $ x$} & \---- & & +\text{ $x$ M} & + \text{$x$ M} \\E & \text{(0.563 - $x$) M} & \---- & & \text{$x$ M} & \text{$x$ M} \end{tabular}`

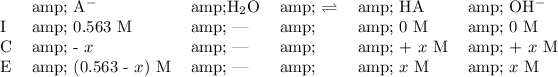
Find [OH⁻] from the given pH:

`\displaystyle \begin{aligned} \text{pH} +\text{pOH} & = 14.00 \\ \\ \text{pOH} & = 14.00 - \text{pH} \\ \\ & = 14.00 - (11.56) \\ \\ & = 2.44 \\ \\ -\log[\text{OH}^-] & = 2.44 \\ \\ [\text{OH}^-] &= 10^(-2.44) \\ \\ & =0.00363 \text{ M}= 3.63* 10^(-3) \text{ M} = x\text{ M}\end{aligned}`

Solve for all species concentrations at equilibrium from the found x value:

`\displaystyle [\text{HA}] = [\text{OH}^-] = 3.63* 10^(-3) \text{ M}`

And:

`\displaystyle \begin{aligned} \ [\text{A}^-] & = 0.563 - 3.63* 10^(-3) \text{ M}\\ \\ & = 0.559\text{ M}\end{aligned}`

Find Kb:

`\displaystyle \begin{aligned} \displaystyle K_b &= \frac{[\text{OH}^-][\text{HA}]}{[\text{A}^-]} \\ \\ & = ((3.63* 10^(-3))(3.63* 10^(-3)))/((0.559))\\ \\ & = 2.36* 10^(-5)\end{aligned}`

Find Ka:

`\displaystyle \begin{aligned} K_a\cdot K_b & = K_w \\ \\ K_a & = (K_w)/(K_b) \\ \\ & = ((1.00 * 10^(-14)))/((2.36* 10^(-5))) \\ \\ &= 4.24* 10^(-10) \end{aligned}`

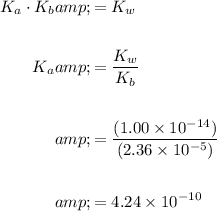
In conclusion:

`\displaystyle K_a = 4.24* 10^(-10)`