Answer:
See step by step explanation
Explanation:
To reconize a geometric sequence, the factor at which one number is greater than the previous number should always be the same
For example,
2,4,8,16,32,64,128,256,512,1024 is a geometric sequence since the next number is always greater than the previous number by a factor of 2
to find the n-th term in a sequence, we can use a formula.
Going back to the example, let's label each number with a term
- 2
- 4
- 8
- 16
- 32
- 64
- 128
- 256
- 512
- 1024
to find the nth term of this specific sequence, we need to find two things
the first number of the sequence, and the factor at which this sequence increases at
the first number is 2, so n1 = 2
each term increases by a factor of 2 (2*2=4, 4*2=8, 8*2=16, 16*2=32, 32*2=64), so the factor is 2
the equation is:
(the initial term)*(the factor)^(the term number - 1)
so,
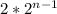 is our equation
is our equation
We can check our equation by plugging in a number
looking back at our list, we see that the 7th term is 128
plug in 7 into out equation
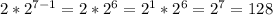 , so our equation works
, so our equation works
Here's a practice problem
for the sequence 3,9,27,81,243,729, what is the factor which the sequence increases at? what's the initial number? what's the equation for this sequence?
a harder practice problem:
for the sequence 2,6,18,54,162,486, what is the factor at which the sequence increases at? what's the intitial number? what's the equation for this sequence? what's the 8th term of this sequence if it were to be continued?