Answer: The required probability is 0.674.
Explanation:
Since we have given that
Number of students in the Spanish class = 38
Number of students in the French class = 27
Number of students in the German class = 16
Number of students in both spanish and French = 14
Number of students in both Spanish and German = 6
Number of students in both French and German = 5
Number of students in all three class = 2
So, it becomes:
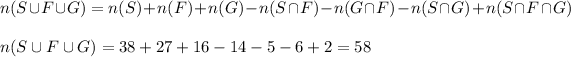
So, Probability that he or she is taking at least one language class is given by
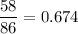
Hence, the required probability is 0.674.