Question

M84, M87, and NGC 4258 all have accretion disks around their central black holes for which the rotational velocities have been measured in HST spectra. In M84, the disk extends 8 pc from the center and exhibits Doppler velocities as large as ±400 km/s with respect to the galaxy's overall radial velocity. In M87, the corresponding figures are 20 pc and 500 km/s. In NGC 4258, the figures are 0.5 ly and 1000 km/s. Calculate the black hole masses to two significant figures. Comment also on the assumptions under which you did your calculation (e.g., orbital plane viewed edge-on; note the appearance of the galaxies and their disks in the notes) and the effect this may have on the accuracy of the answers.

Answer 1

For M84:

M = 590.7 * 10³⁶ kg

For M87:

M = 2307.46 * 10³⁶ kg

Step-by-step explanation:

1 parsec, pc = 3.08 * 10¹⁶ m

The equation of the orbit speed can be used to calculate the doppler velocity:

`v = \sqrt{(GM)/(r) }`

making m the subject of the formula in the equation above to calculate the mass of the black hole:

`M = (v^(2) r)/(G)`.............(1)

For M84:

r = 8 pc = 8 * 3.08 * 10¹⁶

r = 24.64 * 10¹⁶ m

v = 400 km/s = 4 * 10⁵ m/s

G = 6.674 * 10⁻¹¹ m³/kgs²

Substituting these values into equation (1)

`M = (( 4*10^(5)) ^(2) *24.64* 10^(16) )/(6.674 * 10^(-11) )`

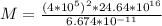
M = 590.7 * 10³⁶ kg

For M87:

r = 20 pc = 20 * 3.08 * 10¹⁶

r = 61.6* 10¹⁶ m

v = 500 km/s = 5 * 10⁵ m/s

G = 6.674 * 10⁻¹¹ m³/kgs²

Substituting these values into equation (1)

`M = (( 5*10^(5)) ^(2) *61.6* 10^(16) )/(6.674 * 10^(-11) )`

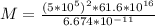
M = 2307.46 * 10³⁶ kg

The mass of the black hole in the galaxies is measured using the doppler shift.

The assumption made is that the intrinsic velocity dispersion is needed to match the line widths that are observed.