Question

A 3.0-Ω resistor is connected in parallel with a 6.0-Ω resistor. This combination is then connected in series with a 4.0-Ω resistor. The resistors are connected across an ideal 12-volt battery. How much power is dissipated in the 3.0-Ω resistor? Group of answer choices

a. 12 w
b. 2.7 w
c. 6.0 w
d. 5.3 w

Answer 1

To solve this problem we must find the values of the equivalent resistances in both section 1 and section 2. Later we will calculate the total current and the total voltage. With the established values we can find the values of the currents in the 3 Ohms resistance and the power there.

The equivalent resistance in section 1 would be

`R_(eq1) = ((3\Omega)(6\Omega))/((3+6)\Omega)`

`R_(eq1) = 2\Omega`

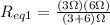
The equivalent resistance in section 2 would be

`R_(eq2) = R_(eq1) +4\Omega`

`R_(eq2) = 6\Omega`

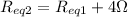
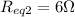
Now the total current will be,

`I_t = (V_t)/(R_(eq2))`

`I_t = (12V)/(6\Omega)`

`I_t = 2.0A`

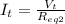
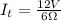
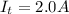
Finally the total Voltage will be,

`V = IR_(eq1)`

`V = (2.0A)(2.0\Omega)`

`V = 4V`

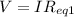
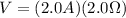
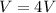
Since the voltage across the 3 and 6 Ohms resistor is the same, because they are in parallel, the current in section 3 would be

`I_(3.0\Omega) = (V)/(R)`

`I_(3.0\Omega) = (4.0V)/(3.0\Omega)`

`I_(3.0\Omega) = 1.3A`

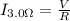
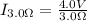
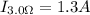
Finally the power ratio is the product between the current and the voltage then,

`P_(3.0\Omega) = I_(3.0\Omega) V`

`P_(3.0\Omega) = (1.3A)(4.0V)`

`P_(3.0\Omega) = 5.3W`

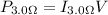
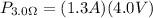
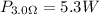
Therefore the correct answer is D.