Question

Two identical horizontal sheets of glass have a thin film of air of thickness t between them. The glass has refractive index 1.40. The thickness t of the air layer can be varied. Light with wavelength λ in air is at normal incidence onto the top of the air film. There is constructive interference between the light reflected at the top and bottom surfaces of the air film when its thickness is 700 nm. For the same wavelength of light the next larger thickness for which there is constructive interference is 980 nm.

a. What is the wavelength λ of the light when it is traveling in air?
b. What is the smallest thickness t of the air film for which there is constructive interference for this wavelength of light?

Answer 1

1.4x10^7m & 98nm

Step-by-step explanation:

Pls the calculation is in the attached file

Answer 2

the wavelength λ of the light when it is traveling in air = 560 nm

the smallest thickness t of the air film = 140 nm

Step-by-step explanation:

From the question; the path difference is Δx = 2t (since the condition of the phase difference in the maxima and minima gets interchanged)

Now for constructive interference;

Δx=
`(m+ (1)/(2) \lambda)`

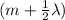
replacing ;

Δx = 2t ; we have:

2t =
`(m+ (1)/(2) \lambda)`

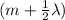
Given that thickness t = 700 nm

Then

2× 700 =
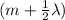`(m+ (1)/(2) \lambda)` --- equation (1)

For thickness t = 980 nm that is next to constructive interference

2× 980 =
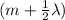`(m+ (1)/(2) \lambda)` ----- equation (2)

Equating the difference of equation (2) and equation (1); we have:'

λ = (2 × 980) - ( 2× 700 )

λ = 1960 - 1400

λ = 560 nm

Thus; the wavelength λ of the light when it is traveling in air = 560 nm

b)

For the smallest thickness
`t_(min) ; \ \ \ m =0`

∴
`2t_(min) =(\lambda)/(2)`

`t_(min) =(\lambda)/(4)`

`t_(min) =(560)/(4)`

`t_(min) =140 \ \ nm`

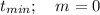
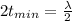
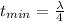
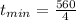
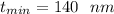
Thus, the smallest thickness t of the air film = 140 nm