Question

Solve the equation for all real values of x. 3tan^2x=3tanx

Answer 1

The equation 3tan²x = 3tanx solved for all real values of x is
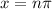`x = n\pi` or
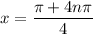`x = (\pi + 4n\pi)/(4)`, where n is an integer

Solving the equation for all real values of x.

From the question, we have the following parameters that can be used in our computation:

3tan²x = 3tanx

This can be expressed as

3tan²x - 3tanx = 0

Factor out 3tanx

3tanx(tanx - 1) = 0

Expand

3tanx = 0 or tanx - 1 = 0

So, we have

tanx = 0 or tanx = 1

Take the arctan of both sides

x = tan⁻¹(0) or x = tan⁻¹(1)

Evaluate the arctan for all real values of x.

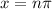`x = n\pi` or
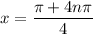`x = (\pi + 4n\pi)/(4)`, where n is an integer

Answer 2

The answer to your question is x₁ = 0° and x₂ = 45°

Explanation:

Data

3tan²x = 3tanx

Process

1.- Equal to zero

3tan²x - 3tanx = 0

2.- Factor by common factor

3tanx(tanx - 1) = 0

3.- Equal to zero each factor

3tanx = 0 tanx - 1 = 0

tanx = 0/3 tanx = 1

tanx = 0 x = 45°

x = 0°