Question

The Nellie Mae organization conducts an extensive annual study of credit card usage by college students. For their 2004 study, they analyzed credit bureau data for a random sample of 1,413 undergraduate students between the ages of 18 and 24. They found that 76% of the students sampled held a credit card. Three years earlier they had found that 83% of undergraduates sampled held a credit card. (Assume that the sample size was similar in 2001.)

1. State the appropriate null and alternative hypotheses for testing whether the proportion of undergraduate students who held a credit card differed between these two years.
2. Conduct an appropriate test of these hypotheses.
3. Report the test statistic and p-value and summarize your conclusion.

Answer 1

1. Null Hypothesis,
`H_0` :
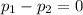`p_1-p_2=0` or
`p_1=p_2`

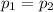
Alternate Hypothesis,
`H_A` :
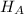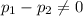`p_1-p_2\\eq 0` or
`p_1\\eq p_2`

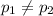
2. Test statistics = 4.63

P-value = 0.00001

3. We conclude that the proportion of undergraduate students who held a credit card differed between these two years.

Explanation:

We are given that the Nellie Mae organization conducts an extensive annual study of credit card usage by college students.

For their 2004 study, they analyzed credit bureau data for a random sample of 1,413 undergraduate students between the ages of 18 and 24. They found that 76% of the students sampled held a credit card. Three years earlier they had found that 83% of undergraduates sampled held a credit card.

Let
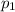`p_1` = population proportion of undergraduate students who held a credit card in year 2001

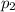`p_2` = population proportion of undergraduate students who held a credit card in year 2004

1. Null Hypothesis,
`H_0` :
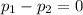`p_1-p_2=0` or
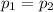`p_1=p_2` {means that the proportion of undergraduate students who held a credit card does not differed between these two years}

Alternate Hypothesis,
`H_A` :
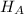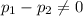`p_1-p_2\\eq 0` or
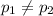`p_1\\eq p_2` {means that the proportion of undergraduate students who held a credit card differed between these two years}

The test statistics that will be used here is Two-sample z proportion statistics;

T.S. =
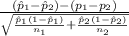`\frac{(\hat p_1-\hat p_2)-(p_1-p_2)}{\sqrt{(\hat p_1(1-\hat p_1))/(n_1) +(\hat p_2(1-\hat p_2))/(n_2)} }` ~ N(0,1)

where,
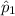`\hat p_1` = sample proportion of undergraduate students who held a credit card in 2001 = 83%

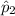`\hat p_2` = sample proportion of undergraduate students who held a credit card in 2004 = 76%

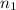`n_1` = sample of students surveyed in 2001 = 1,413

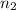`n_2` = sample of students surveyed in 2004 = 1,413

So, test statistics =
`\frac{(0.83-0.76)-(0)}{\sqrt{(0.83(1-0.83))/(1,413) +(0.76(1-0.76))/(1,413)} }`

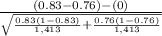
= 4.63

2. Hence, the value of test statistics is 4.63.

Also, P-value is given by the following formula;

P-value = P(Z > 4.63) = 1 - P(Z
`\leq` 4.63)

= 1 - 0.99999 = 0.00001

3. Since in the question we are not given the level of significance so we assume it to be 5%. Now at 5% significance level, the z table gives critical values between -1.96 and 1.96 for two-tailed test. Since our test statistics is does not lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the proportion of undergraduate students who held a credit card differed between these two years.