Answer:
The refraction angle of the light in the liquid is 8.40 degrees.
Step-by-step explanation:
Given:
A ray of light passing through air to liquid.
Air is medium 1 and liquid is medium 2.
Angle of incidence
 = 13°
= 13°
Refractive index,
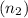 = 1.54
= 1.54
We have to find the angle of refraction:
Let the angle of refraction be "
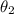 " .
" .
Formula to be used:
⇒
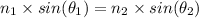
Note:
Index of refraction of air
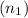 = 1
= 1
Accordingly:
Using Snell's law and plugging the values.
⇒
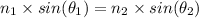
⇒
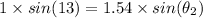
⇒
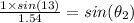
⇒
 ...sin(13) =0.2249
...sin(13) =0.2249
⇒

⇒
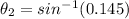
⇒
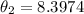 degrees.
degrees.
⇒
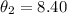 degrees ...Rounded to 2 decimal place.
degrees ...Rounded to 2 decimal place.
The refraction angle of the light in the liquid is 8.40 degrees.