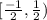Question

Consider the series

\sum_{n=1}^{\infty} \frac{(2 x)^n}{n}.

Find the interval of convergence of this power series by first using the ratio test to find its radius of convergence and then testing the series' behavior at the endpoints of the interval specified by the radius of convergence.
interval of convergence =

Answer 1

Explanation:

Recall the ratio test. Given a series
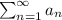`\sum_(n=1)^(\infty)a_n` if

`\lim_(n\to \infty) \left|(a_(n+1))/(a_n)\right|<1`

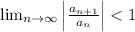
Then, the series is absolutely convergent.

We will use this to the given series
`\sum_(n=1)^(\infty) ((2 x)^n)/(n)`, where
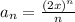`a_n = ((2 x)^n)/(n)`. Then, we want to find the values for which the series converges.

So

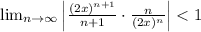`\lim_(n\to \infty) \left|((2x)^(n+1))/(n+1)\cdot (n)/((2x)^n)\right|<1`, which gives us that

`|2x|\cdot\lim_(n\to \infty) (n)/(n+1)<1`

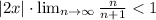
We have that
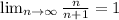`\lim_(n\to \infty) (n)/(n+1)=1`. Then, we have that

`|2x|<1`,

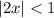which implies that |x|<1/2. So for
`x \in (-1/2,1/2)` the series converges absolutely.

We will replace x by the endpoints to check convergence.

Case 1, x=1/2:

In this case we have the following series:

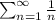`\sum_(n=1)^(\infty) (1)/(n)` which is the harmonic series, which is know to diverge.

Case 2, x=-1/2:

In this case we have the following series:

`\sum_(n=1)^(\infty) ((-1)^n)/(n)`

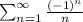
This is an alternating series with
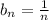`b_n = (1)/(n)`. Recall the alternating series test. If we have the following

`\sum_(n=1)^\infty (-1)^nb_n` and
`b_n` meets the following criteria : bn is positive, bn is a decreasing sequence and it tends to zero as n tends to infinity, then the series converge.

Note that in this case,
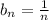`b_n = (1)/(n)` si always positive, its' limit is zero as n tends to infinity and it is decreasing, hence the series converge.

So, the final interval of convergence is

`[(-1)/(2), (1)/(2))`

Answer 2

(-\infty,-1/2) U (1/2,+\infty)

Explanation:

You have the following series:

`\sum_(n=1)^(\infty) ((2 x)^n)/(n)`

You calculate the radius of convergence by using the formula:

`R= \lim_(n \to \infty) |(a(x)_n)/(a(x)_(n+1))|= \lim_(n \to \infty) |(((2x)^n)/(n))/(((2x)^(n+1))/(n+1))|\\\\=\lim_(n \to \infty) |(((2x)^n)/(n))/(((2x)^n(2x))/(n+1))|=\lim_(n \to \infty)|(n+1)/(2xn)|=|(1)/(2x)|\lim_(n \to \infty)|1+(1)/(n)|=|(1)/(2x)|`

The radius of convergence is R=1/2x.

Hence, the interval of convergence is

|2x| < 1

|x| < 1/2

By evaluating in the extrems of the interval:

`\sum_(n=1)^(\infty) ((2 ((1)/(2)))^n)/(n)=\sum_(n=1)^(\infty) ((1)^n)/(n)=0\\\\\sum_(n=1)^(\infty) ((2 (-(1)/(2)))^n)/(n)=\sum_(n=1)^(\infty) ((-1)^n)/(n)`

for x=-1/2 we obtain an Alternating Harmonic Series, for x=1/2 we obtain the divergent harmonic series. Thus the interval is:

(-\infty,-1/2) U [1/2,+\infty)