Answer:
The correct answer is the seventh term of the sequence is 3
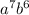 and the sequence is infinite.
and the sequence is infinite.
Explanation:
The sequence discussed here is infinite. Here there is no bound on the value of n therefore making it an infinite sequence.
The nth term of the sequence is given by
 = 3
= 3
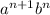 , where n is greater than equal to 0.
, where n is greater than equal to 0.
The sequence would look like this:
3
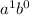 , 3
, 3
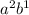 , 3
, 3
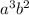 , 3
, 3
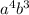 , 3
, 3
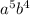 , 3
, 3
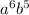 , 3
, 3
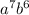 ...
...
The seventh term of the sequence is given by 3
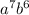 .
.
This sequence is infinite.